在数学领域，结合律与分配律是基本的运算规律，对于小学生学习数学以及后续的数学学习都具有重要的意义，本文将围绕这两个主题展开讨论，帮助读者深入理解其含义、应用及实例。

结合律

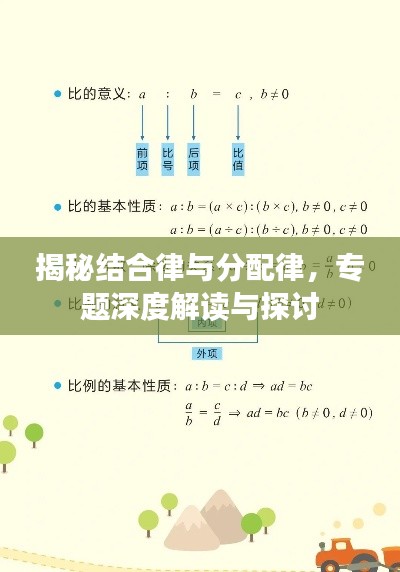
1、定义：结合律是指在一个多步骤运算中，无论括号如何分组，只要运算顺序不变，计算结果就不会改变，加法的结合律可以表示为：(a+b)+c=a+(b+c)。

2、应用：结合律在解决实际问题时非常有用，尤其是在处理复杂运算时，可以通过改变括号的位置来简化计算过程，在计算大量数字的和时，我们可以将相近的数字组合在一起，使得计算更为简便。

分配律

1、定义：分配律是关于乘法和加法的一个基本运算定律，它表示一个二项式与一个多项式相乘时，可以将它们分别相乘后再相加或相减，分配律可以表示为：a(b+c)=ab+ac。

2、应用：分配律在实际生活中有广泛的应用，在解决实际问题时，我们可以利用分配律将复杂的运算过程简化为多个简单的运算步骤，在计算面积时，我们可以利用分配律将复杂的图形分割为简单的图形进行计算。

结合律与分配律的结合应用

在实际问题中，结合律和分配律常常需要结合使用，通过灵活运用这两个定律，我们可以将复杂的运算过程简化为一系列简单的步骤，从而提高计算效率和准确性，在计算面积时，我们可以先利用分配律将大图形分割为若干个小图形，再利用结合律对每个小图形的面积进行计算和组合。

专题实例分析

假设我们有一组数字：1, 2, 3, ..., 99, 100，我们需要计算这些数字的总和，如果直接相加，工作量会非常大，这时，我们可以利用结合律和分配律来简化计算过程，我们可以将这些数字分为成对出现的数字与奇数数字两部分，然后分别计算它们的和，利用分配律将两个部分的和相加得到最终结果，这样，计算过程大大简化，提高了计算效率。

结合律与分配律是数学中的基本运算规律，对于解决实际问题具有重要意义，通过灵活运用这两个定律，我们可以将复杂的运算过程简化为一系列简单的步骤，提高计算效率和准确性，在实际问题中，我们需要结合使用这两个定律来简化计算过程，从而更好地解决实际问题。

建议与展望

对于学习者来说，要深入理解结合律与分配律的含义和应用，需要通过大量的实践来加深理解，建议学习者多做一些相关练习题，通过实际操作来巩固知识，还可以尝试将这些知识应用到实际生活中，解决一些实际问题，随着人工智能技术的发展，我们可以利用计算机程序来验证和拓展结合律与分配律的应用，为数学研究和实际应用提供更多可能性，结合律与分配律是数学中的宝贵财富，值得我们深入学习和探索。